¶ 二叉树与二叉搜索树(BST)

¶ 前瞻

二叉树的特征
- [题]节点数计算；
- 满二叉树/完美二叉树的定义；
- 完全二叉树的定义；
什么是二叉搜索树(Binary Search Tree)
- BST的查找是很快的
- BST的删除是非常麻烦的
- BST的功能实现

¶ 二叉树基本概念

¶ 特征

暂缺

- [题]节点数计算； - 满二叉树/完美二叉树的定义； - 完全二叉树的定义；

¶ 小结

最底部没有延展任何节点的是叶节点
度为2的非叶节点：节点有2个向下延展的节点
满二叉树：即所有的非叶节点度为2

¶ BST特点，封装与实现

¶ 二叉搜索树的定义

二叉搜索树是一颗二叉树, 可以为空；如果不为空，满足以下性质：

非空左子树的所有键值小于其根结点的键值。
非空右子树的所有键值大于其根结点的键值。
左、右子树本身也都是二叉搜索树。

¶ BST用链表实现是较佳实践

BST的组成
- Node : { left:Node, key:any, right:Node }
- root : Node


class Node {
  constructor(key) {
    // 创建结点构造函数
    this.key = key
    this.left = null
    this.right = null
  }
}
class BinarySearchTree {
  // 保存根的属性
    this.root = null
}
复制成功

1
2
3
4
5
6
7
8
9
10
11
12
13

BST的查找是很快的
BST的删除是非常麻烦的

¶ 向树中插入数据

使用递归插入数据是最方便的方法

class Node {
  constructor(key) {
    this.key = key
    this.left = null
    this.right = null
  }
}
class BinarySearchTree {
  root = null
  
  //插入数据，对外暴露的方法
  insert(key) {
    let newNode = new Node(key)
    
    //this.root存在？
    if(!this.root) {
      this.root = newNode
    }else {
      // 递归开始
      this.insertNode(this.root, newNode)
    }
  }
    //在递归的过程中，插入的数据要么往左走，要么往右走。总能插入中作叶子元素的
  insertNode(node, newNode) {
    let { key, left,right } = node
    
    if(newNode.key < key) {
      //向左查找
      if(node.left === null) {
        // 递归结束
        node.left = newNode
      }else {
        // 递归继续
        this.insertNode(node.left, newNode)
      }
    }else if(newNode.key > key){
      //向右查找
      if(node.right === null) {
        node.right = newNode
      }else {
        this.insertNode(node.right, newNode)
      }
    }else {
      console.error(`键值相等`)
    }
  }
}
复制成功

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

// 测试代码
class Node {
  constructor(key) {
    this.key = key
    this.left = null
    this.right = null
  }
}
class BinarySearchTree {
  root = null
  
  //插入数据，对外暴露的方法
  insert(key) {
    let newNode = new Node(key)
    
    //this.root存在？
    if(!this.root) {
      this.root = newNode
    }else {
      // 递归开始
      this.insertNode(this.root, newNode)
    }
  }
    //在递归的过程中，插入的数据要么往左走，要么往右走。总能插入中作叶子元素的
  insertNode(node, newNode) {
    let { key, left,right } = node
    
    if(newNode.key < key) {
      //向左查找
      if(node.left === null) {
        // 递归结束
        node.left = newNode
      }else {
        // 递归继续
        this.insertNode(node.left, newNode)
      }
    }else if(newNode.key > key){
      //向右查找
      if(node.right === null) {
        node.right = newNode
      }else {
        this.insertNode(node.right, newNode)
      }
    }else {
      console.error(`键值相等`)
    }
  }
}
复制成功

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

¶ BST-遍历

三种遍历方式：

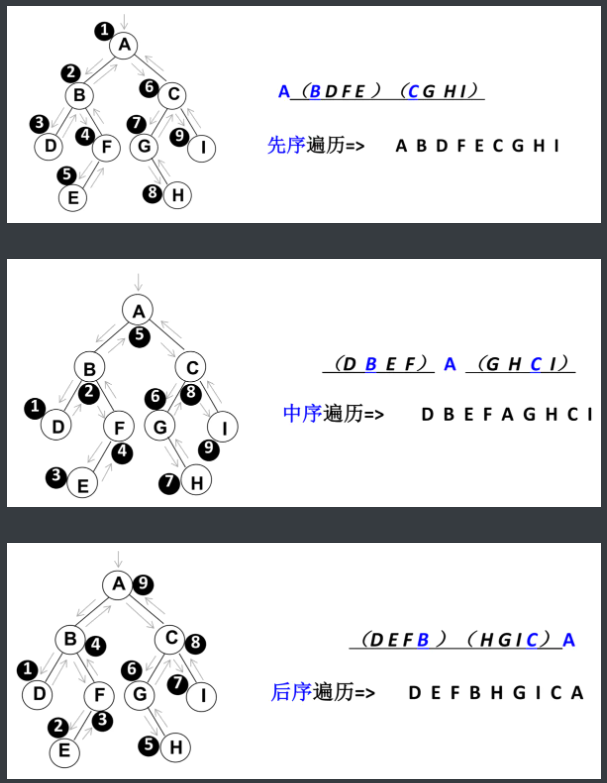
中序遍历的中是啥含义：

实现层面上-handler在递归代码中的位置；
结果层面上-根节点在遍历之后会在什么位置出现

// 先序遍历
BinarySerachTree.prototype.preOrderTraversal = function (handler) {
    this.preOrderTranversalNode(this.root, handler)
}

BinarySerachTree.prototype.preOrderTranversalNode = function (node, handler) {
    if (node !== null) {
        // 1.打印当前经过的节点
        handler(node.key)
        // 2.遍历所有的左子树
        this.preOrderTranversalNode(node.left, handler)
        // 3.遍历所有的右子树
        this.preOrderTranversalNode(node.right, handler)
    }
}

// 中序遍历
BinarySerachTree.prototype.inOrderTraversal = function (handler) {
    this.inOrderTraversalNode(this.root, handler)
}

BinarySerachTree.prototype.inOrderTraversalNode = function (node, handler) {
    if (node !== null) {
        this.inOrderTraversalNode(node.left, handler)
        // 2.打印当前经过的节点
        handler(node.key)
        this.inOrderTraversalNode(node.right, handler)
    }
}

// 后序遍历
BinarySerachTree.prototype.postOrderTraversal = function (handler) {
    this.postOrderTraversalNode(this.root, handler)
}

BinarySerachTree.prototype.postOrderTraversalNode = function (node, handler) {
    if (node !== null) {
        this.postOrderTraversalNode(node.left, handler)
        this.postOrderTraversalNode(node.right, handler)
        handler(node.key)
    }
}
复制成功

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

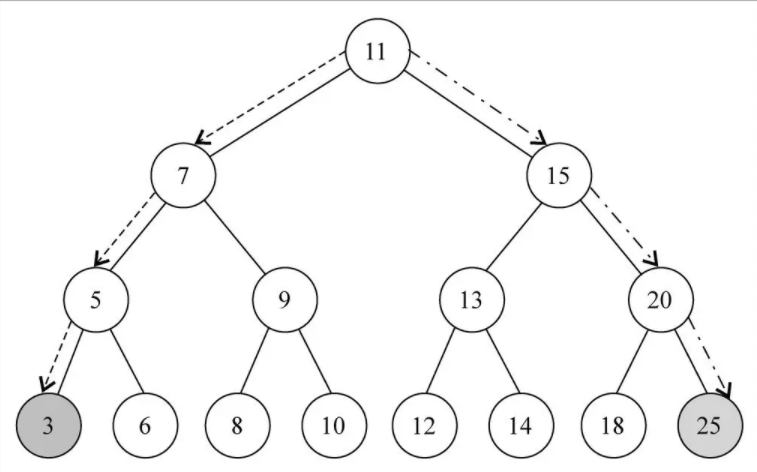
¶ 最大值&最小值

二叉搜索树的最左边的值和最右边的值。用循环，一直向左找，一直向右找。

代码依次向左找到最左边的结点就是最小值,
代码依次向右找到最右边的结点就是最大值.

// 获取最大值和最小值
BinarySerachTree.prototype.min = function () {
    var node = this.root
    while (node.left !== null) {
        node = node.left
    }
    return node.key
}

BinarySerachTree.prototype.max = function () {
    var node = this.root
    while (node.right !== null) {
        node = node.right
    }
    return node.key
}
复制成功

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

¶ 搜索特定的值

二叉搜索树不仅仅获取最值效率非常高, 搜索特定的值效率也非常高.
特定的值不断与新的current节点比较，值比较小则往左。

// 搜索特定的值-递归
BinarySerachTree.prototype.search = function (key) {
    return this.searchNode(this.root, key)
}

BinarySerachTree.prototype.searchNode = function (node, key) {
    // 1.如果传入的node为null那么, 那么就退出递归
    if (node === null) {
        return false
    }

    // 2.判断node节点的值和传入的key大小
    if (node.key > key) { // 2.1.传入的key较小, 向左边继续查找
        return this.searchNode(node.left, key)
    } else if (node.key < key) { // 2.2.传入的key较大, 向右边继续查找
        return this.searchNode(node.right, key)
    } else { // 2.3.相同, 说明找到了key
        return true
    }
}
复制成功

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

// 搜索特定的值-循环
BinarySerachTree.prototype.search = function (key) {
    var node = this.root
    while (node !== null) {
        if (node.key > key) {
            node = node.left
        } else if (node.key < key) {
            node = node.right
        } else {
            // 找到了匹配的叶节点
            return true
        }
    }
    // 找到某一个叶节点,仍未找到特定的值
    return false
}
复制成功

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

¶ BST-删除

查找要删除的节点
分类讨论(if..else if..else if...else)
1. 目标节点没有子节点
2. 目标节点仅1个子节点
3. 目标节点有2个子节点（度为2的非叶节点）

¶ 1. 查找要删除的节点

// BinarySerachTree.prototype.remove
// 希望删除，需要用三个变量
var current = this.root
var parent = this.root
var isLeftChild = true
// 循环
while (current.key !== key) {
    parent = current
    if (key < current.key) {
        isLeftChild = true
        current = current.left
    } else {
        isLeftChild = false
        current = current.right
    }

    // 如果发现current已经指向null, 那么说明没有找到要删除的数据
    if (current === null) return false
    
    // 得到三个变量，已查出目标current节点。...
}
复制成功

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

¶ 2.1.删除的结点是叶结点

// 2.1.删除的结点是叶结点
if (current.left === null && current.right === null) {
    if (current == this.root) {
        this.root == null
    } else if (isLeftChild) {
        parent.left = null
    } else {
        parent.right = null
    }
}
复制成功

1
2
3
4
5
6
7
8
9
10

¶ 2.2.删除有一个子节点的节点

// 2.2.删除有一个子节点的节点
else if (current.right === null) {
    if (current == this.root) {
        this.root = current.left
    } else if (isLeftChild) {
        parent.left = current.left
    } else {
        parent.right = current.left
    }
} 
else if (current.left === null) {
    if (current == this.root) {
        this.root = current.right
    } else if (isLeftChild) {
        parent.left = current.right
    } else {
        parent.right = current.right
    }
}
复制成功

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

¶ 2.3. 删除目标节点有2个子节点：寻找前驱 | 后继

规律总结：如果要删除的节点有两个子节点，甚至子节点还有子节点，这种情况下需要从要删除节点下面的子节点中找到一个合适的节点，来替换当前的节点。

若用 current 表示需要删除的节点，则合适的节点指的是：

current 节点的前驱: current 左子树中比 current 小一点点的节点，即 current 左子树中的最大值；
**current 节点的后继: **current 右子树中比 current 大一点点的节点，即 current 右子树中的最小值；

删除这个节点的思路：

// 2.3.删除有两个节点的节点
else {
    // 1.获取后继节点
    var successor = this.getSuccessor(current)
    
    // 2.判断是否是根节点
    if (current == this.root) {
        this.root = successor
    } else if (isLeftChild) {
        parent.left = successor
    } else {
        parent.right = successor
    }
    
    // 3.将删除节点的左子树赋值给successor
    successor.left = current.left
}
复制成功

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

// 找后继的方法
// (循环,从current.right开始一直迭代current/successor等三个变量,一直往左找最小值)

BinarySerachTree.prototype.getSuccessor = function (delNode) {
    // 1.使用变量保存临时的节点
    var successorParent = 
    var successor = delNode
    var current = delNode.right // 要从右子树开始找

    // 2.寻找节点
    while (current != null) {
        successorParent = successor
        successor = current
        current = current.left
    }

    // 3.如果是删除图中15的情况, 还需要如下代码
    	// ps:此时后继节点是18
    	// 18!=20
    	// 后继节点父亲的left指针不再指向后继节点，指向 后继节点.right(图中的19)
    	// 后继节点的right指针数据已存好，改为指向 delNode.right(图中的20)
    if (successor != delNode.right) {
        successorParent.left = successor.right
        successor.right = delNode.right
    }
    
    return successor
}
复制成功

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

getSuccessor()后继节点图注：

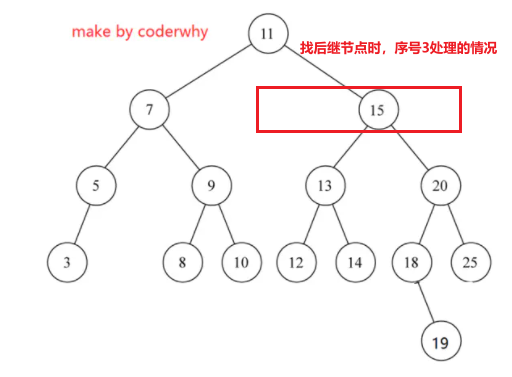
¶ 删除节点完整代码

// 删除结点
BinarySerachTree.prototype.remove = function (key) {
    // 1.定义临时保存的变量
    var current = this.root
    var parent = this.root
    var isLeftChild = true

    // 2.开始查找节点
    while (current.key !== key) {
        parent = current
        if (key < current.key) {
            isLeftChild = true
            current = current.left
        } else {
            isLeftChild = false
            current = current.right
        }

        // 如果发现current已经指向null, 那么说明没有找到要删除的数据
        if (current === null) return false
    }

    // 3.删除的结点是叶结点
    if (current.left === null && current.right === null) {
        if (current == this.root) {
            this.root == null
        } else if (isLeftChild) {
            parent.left = null
        } else {
            parent.right = null
        }
    }

    // 4.删除有一个子节点的节点
    else if (current.right === null) {
        if (current == this.root) {
            this.root = current.left
        } else if (isLeftChild) {
            parent.left = current.left
        } else {
            parent.right = current.left
        }
    } else if (current.left === null) {
        if (current == this.root) {
            this.root = current.right
        } else if (isLeftChild) {
            parent.left = current.right
        } else {
            parent.right = current.right
        }
    }

    // 5.删除有两个节点的节点
    else {
        // 1.获取后继节点
        var successor = this.getSuccessor(current)

        // 2.判断是否是根节点
        if (current == this.root) {
            this.root = successor
        } else if (isLeftChild) {
            parent.left = successor
        } else {
            parent.right = successor
        }

        // 3.将删除节点的左子树赋值给successor
        successor.left = current.left
    }

    return true
}

// 找后继的方法
BinarySerachTree.prototype.getSuccessor = function (delNode) {
    // 1.使用变量保存临时的节点
    var successorParent = delNode
    var successor = delNode
    var current = delNode.right // 要从右子树开始找

    // 2.寻找节点
    while (current != null) {
        successorParent = successor
        successor = current
        current = current.left
    }

    // 3.如果是删除图中15的情况, 还需要如下代码
    if (successor != delNode.right) {
        successorParent.left = successor.right
        successor.right = delNode.right
    }
    
    return successor
}
复制成功

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95

晓露寝安浅云逍遥十漾轻拟

¶ # 二叉树与二叉搜索树(BST)

¶ # 前瞻

¶ # 二叉树基本概念

¶ # 特征

¶ # 小结

¶ # BST特点，封装与实现

¶ # 二叉搜索树的定义

¶ # BST用链表实现是较佳实践

¶ # 向树中插入数据

¶ # BST-遍历

¶ # 最大值&最小值

¶ # 搜索特定的值

¶ # BST-删除

¶ # 1. 查找要删除的节点

¶ # 2.1.删除的结点是叶结点

¶ # 2.2.删除有一个子节点的节点

¶ # 2.3. 删除目标节点有2个子节点：寻找前驱 | 后继

¶ # 删除节点完整代码